La nueva traducción de Sans dessus-dessous de Julio Verne (Del revés, Alba Editorial, 2021) incluye una parte de la obra hasta ahora inédita en castellano: el «Capítulo suplementario» en el que el ingeniero y matemático Paul Albert Badoureau desgrana con sumo detalle los razonamientos científicos en los que se apoya la trama. En este artículo, nos acercaremos a la revisión técnica de la obra y a los entresijos de este curioso anexo que sirve de puente entre la ciencia ficción verniana y la divulgación científica.
El libro Breve historia del tiempo catapultó a la fama a Stephen Hawking, convirtiéndolo en un auténtico fenómeno de ventas; un hecho que lo sacaría de los apuros económicos derivados de las limitaciones a las que lo sometía su enfermedad. Aunque ya era reputado y ampliamente conocido en el plano académico, no tenía gran experiencia en la divulgación, así que presentó un libro repleto de fórmulas y complejas explicaciones. Los editores tumbaron aquel proyecto inicial, pues cada fórmula diezmaría las ventas. Solo dejaron una: E = mc2, la famosa ecuación de Einstein que relaciona energía y masa. Dejaron diagramas explicativos y sencillas gráficas, que son otra forma de matematizar la naturaleza.
La realidad humana es así, aunque le pese a Hawking y a quienes nos gustan las expresiones algebraicas. Queremos rapidez y no calentarnos la cabeza.
La realidad humana es así, aunque le pese a Hawking y a quienes nos gustan las expresiones algebraicas. Queremos rapidez y no calentarnos la cabeza. En el otro extremo, El camino de la realidad de Roger Penrose (Debate, 2006) nos bombardea con todo tipo de fórmulas complejas, en un ladrillo de más de mil páginas. Y, sin embargo, se supone que es divulgación. En el mundo editorial hay comida para todos. Si bien el texto de Hawking está al alcance de cualquiera que se ponga manos a la obra, el de Penrose puede atragantársele incluso a estudiantes de Física.
Porque la trama del libro es intentar modificar el eje de la Tierra, poner el mundo del revés, patas arriba. O manga por hombro, como la habitación de un adolescente.
No hay que llegar a tanto, tal vez un anexo con fórmulas que apoye el texto es la solución para que todos los lectores estén contentos. Es lo que hizo Julio Verne con su libro Sans dessus-dessous. Dos traducciones anteriores al castellano lo titularon El secreto de Maston y Sin arriba ni abajo. En esta magnífica nueva traducción de Elena Bernardo se ha titulado con acierto como Del revés. Porque la trama del libro es intentar modificar el eje de la Tierra, poner el mundo del revés, patas arriba. O manga por hombro, como la habitación de un adolescente. J. T. Maston, el protagonista, idea un cañón que trasladará el eje de la Tierra a 3000 km de los polos actuales. O eso pretendía.
Julio Verne no era un escritor de ciencia ficción cualquiera, se apoyaba en el verdadero conocimiento científico para tapar bocas.
Sin embargo, Julio Verne ahoga el colosal intento de la empresa, pues un error de cálculo del protagonista muestra que no podrá modificarse el eje de la Tierra en la cuantía calculada. Decirlo así a las bravas está muy bien. Pero Julio Verne no era un escritor de ciencia ficción cualquiera, se apoyaba en el verdadero conocimiento científico para tapar bocas:
«La novela que acabamos de presentar al público, al igual que todas nuestras obras anteriores, reposa en bases serias pese a su apariencia ultrafantástica».
Que el lector duerma tranquilo: para llegar a conseguir lo que había previsto, harían falta «un trillón de cañones parecidos al artefacto horadado en el macizo del Kilimanjaro».
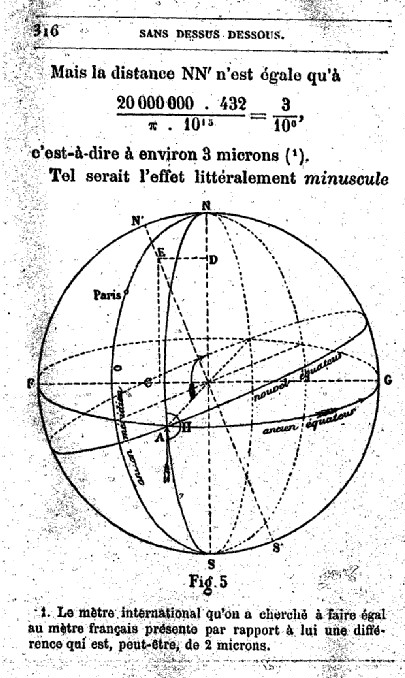
Y para demostrarlo y acallar de antemano esas posibles críticas, acudió a su amigo Jean Paul Albert Badoureau, matemático e ingeniero de minas. En palabras del propio Verne, «lo que la novela muestra, este trabajo lo demuestra». En algo más de 20 páginas repletas de fórmulas, Badoureau prueba que Verne está en lo cierto. Lo hace en el famoso «Capítulo suplementario» traducido al castellano por primera vez por Alba Editorial. En un enfoque muy realista, un despiste le hace anotar a Maston 40 000 m para la longitud de la circunferencia de la Tierra, en vez de 40 000 km. Esto supone un error de tres ceros respecto al orden de magnitud (debería haber escrito 40 000 000 m). Badoureau demuestra con varias ecuaciones y dibujos que la propagación de este error se multiplica hasta tal punto que los polos se desplazarían solo 3 micras, en vez de los 3000 km previstos. Pero que el lector duerma tranquilo: para llegar a conseguir lo que había previsto, haría falta «un trillón de cañones parecidos al artefacto horadado en el macizo del Kilimanjaro».
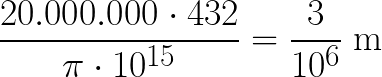
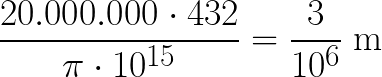

Recibir un encargo técnico de una editorial como Alba Editorial es todo un reto, pues hablamos de una editorial que da cabida a grandes clásicos con ediciones muy cuidadas. Y, sin embargo, no encontraremos títulos con ecuaciones matemáticas o con razonamientos científicos complejos, lo que hace caer la responsabilidad sobre uno mismo. Un peso tremendo, pues había que tomar decisiones en la edición de las fórmulas. Y cuando se toman decisiones, se aceptan unos criterios en detrimento de otros, a pesar de que ambos te parezcan relativamente correctos. Hemos usado LaTeX en la edición, algo poco habitual en un libro de estas características, pero que le da el rigor que merece. Algunos detalles importantes que el lector profano ignora respecto a las decisiones tomadas: uso de punto medio (·) para expresar productos (multiplicaciones), uso de punto bajo (.) para expresar separación de grupos de tres cifras (en los textos científicos suelen usarse espacios, por ejemplo, 40 000 000 m), uso de un espacio simple entre la cifra y la unidad, uso de la unidad de medida en los casos en que Badoureau había prescindido de ella (para ayudar en la interpretación) y aceptación de la expresión coloquial micra en referencia al micrómetro (millonésima parte de un metro).

Obviamente, una tarea que me encomendé a mí mismo fue repasar todos los cálculos y razonamientos matemáticos presentes en el texto.
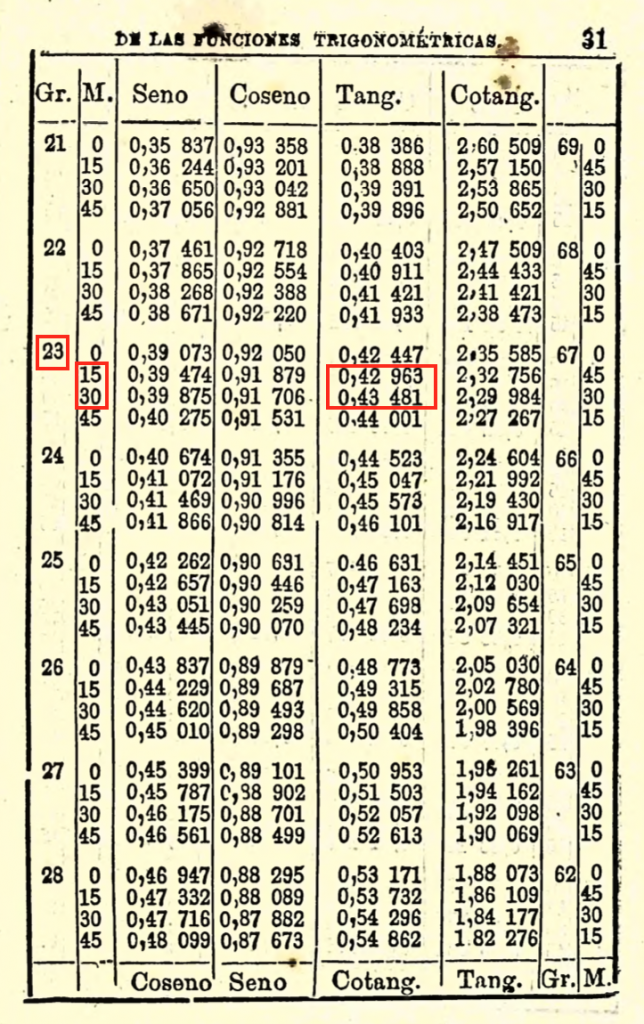
Obviamente, una tarea que me encomendé a mí mismo fue repasar todos los cálculos y razonamientos matemáticos presentes en el texto. Encontré una cifra con un error minúsculo, pero que nos hace viajar al calor de otra época; aquella en la que las calculadoras eran libros con interminables hojas repletas de tablas trigonométricas, logarítmicas, de intereses, etc. Una de las entradas de estas maravillosas tablas era tangentes de ángulos. El caso es que en la página 212 de nuestra edición actual (Alba, 2021) aparece tan α = 0,432. La persona que desea saber cuál es el ángulo cuya tangente vale 0,432 debe buscar dicho valor en aquellas tablitas de la época. Se lleva una sorpresa muy habitual: ese número no está. Hay que hacer aproximaciones, puesto que sí que aparecen los valores 0,429 63 y 0,434 81 (ver imagen). Por tanto, el ingeniero lo que hizo fue aproximar a la baja y quedarse con el primer valor (0,429 63), por lo que le sale un ángulo de 23º 15’ (ver tabla que se adjunta). Sin embargo, el valor real del ángulo sería 23º 21’ 52’’, si nos da el arrebato de hacerlo con una calculadora. Escrito en radianes, el valor que da el amigo de Verne es de 0,407 (23º 20’), pero debería ser 0,408 (23º 21’ 52’’). La diferencia es mínima, pues ambos aproximados a dos decimales sería 0,41, pero es una curiosidad que evidencia las limitaciones de cálculo de la época y que, sin embargo, muestra precisiones sorprendentes. Una posibilidad también habría sido que la errata estuviese en la propia tabla de consulta o que la vista de Badoureau se fuese a otra fila, es decir, un despiste parecido al de Maston en la propia historia del libro. Habría sido una maravillosa ironía.
Durante todo el texto y no solo en el capítulo suplementario, aparecen algunos tecnicismos que no suponen distracción al lector.
Durante todo el texto y no solo en el capítulo suplementario, aparecen algunos tecnicismos que no suponen distracción al lector. Si acaso, algunos nombres de sustancias químicas que han caído en desuso y cuyo equivalente actual se refleja en notas al pie, como el ácido azoico, que es el actual ácido nítrico, o el prusiato amarillo de potasa, al que hoy llamamos ferrocianuro de potasio. Todo lo que encuentre el lector puede ser visto con una actualidad apabullante. Así que, no tenga miedo de leer este libro y guarde el capítulo de Badoureau como una interesante rareza, a la par que una novedad en castellano.


Eugenio Manuel Fernández Aguilar
Eugenio Manuel Fernández Aguilar (Sevilla, 1976) es licenciado en Física por la Universidad de Sevilla y actualmente ejerce de profesor de Ciencias en Secundaria. Además, forma parte del equipo de autores de libros de texto de Ciencias y Matemáticas para varias editoriales, como Algaida-Anaya o Edebé.
Respecto a la divulgación científica, Eugenio ha impartido numerosas conferencias, cursos, ponencias y talleres sobre la historia de la ciencia. También, en este ámbito, ha publicado varios libros, entre los que se encuentran tres biografías científicas traducidas al italiano, francés, portugués y ruso: La conspiración lunar ¡vaya timo! (Laetoli), Arquímedes (RBA, NG), Ampère (RBA, NG), Boyle (RBA, NG), Eso no estaba en mi libro de historia de la ciencia (Almuzara) y Los renglones torcidos de la ciencia (Antoni Bosch).
Asimismo, Eugenio ha participado con sus poemas en diversas antologías y actualiza constantemente sus blogs Ciencia en el XXI y Ciencia en blanco y negro.